Encuentran soluci¨®n al problema del camino m¨¢s corto
Investigadores de la Universidad de Copenhague encuentran un algoritmo ¡°que resuelve el problema en un tiempo pr¨¢cticamente lineal¡± y permite pesos negativos.

Un grupo de investigadores de la Universidad de Copenhague (Dinamarca) ha encontrado la soluci¨®n a un acertijo que ha dejado perplejos a los expertos durante d¨¦cadas. El objetivo del problema de la ruta m¨¢s corta de fuente ¨²nica es encontrar las rutas m¨¢s cortas entre dos v¨¦rtices o nodos para que la suma de los pesos de las aristas que constituyen el recorrido sea la m¨ªnima.
En el caso planteado, los v¨¦rtices son poblaciones (los nodos son, por ejemplo, ciudades) y los pesos de las aristas es el tiempo que empleamos en desplazarnos de un punto a otro. ¡°Descubrimos un algoritmo que resuelve el problema en un tiempo pr¨¢cticamente lineal, de la manera m¨¢s r¨¢pida posible. Es un problema algor¨ªtmico fundamental que se estudia desde la d¨¦cada de 1950 y se ense?a en todo el mundo. Esta fue una de las razones que nos impuls¨® a resolver¡±, explica el profesor asociado Christian Wulff-Nilsen.
La nueva f¨®rmula hallada resuelve el problema en casi la misma cantidad de tiempo que el algoritmo de Dijkstra, pero tambi¨¦n permite pesos de borde negativos. Ya existen algoritmos de caminos m¨ªnimos que permiten estudiar costes de trayecto diferentes, como la distancia, el tiempo de viaje, el coste generalizado, etc. Estos se usan en una amplia gama de aplicaciones y tecnolog¨ªas como Google Maps, que nos gu¨ªa y orienta a trav¨¦s de paisajes y ciudades.
El a?o pasado, Wulff-Nilsen hizo otro avance con un resultado que abordaba c¨®mo encontrar el camino m¨¢s corto en una red que cambia con el tiempo. Su soluci¨®n al acertijo reciente se basa en ese trabajo. Resolver el acertijo ¡°puede reducir el consumo de bater¨ªa de los coches el¨¦ctricos y hacer la vida m¨¢s dif¨ªcil para los especuladores de divisas en el futuro¡±, informa la universidad en un comunicado.
Pesos negativos y ahorro energ¨¦tico
¡°Estamos agregando una dimensi¨®n que los algoritmos anteriores no tienen. Esta dimensi¨®n nos permite ver lo que llamamos pesos negativos. Un ejemplo pr¨¢ctico de esto puede ser con referencia a las colinas en una red de carreteras, lo cual es bueno saber si tienes un auto el¨¦ctrico que se carga mientras viajas cuesta abajo¡±, explica Wulff-Nilsen.
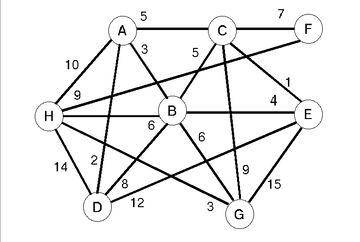
En el problema de la ruta m¨¢s corta de fuente ¨²nica, la red se representa como un grafo formado por nodos y conexiones entre ellos, llamados aristas. Cada borde tiene una direcci¨®n (por ejemplo, esto se puede usar para representar carreteras de un solo sentido), as¨ª como un peso, que expresa lo caro que es viajar a lo largo de ese borde. Si todos los pesos de los bordes son no negativos, el problema se puede resolver en un tiempo pr¨¢cticamente lineal con un algoritmo cl¨¢sico de Dijkstra, que pretende encontrar el camino de la longitud m¨ªnima de un v¨¦rtice origen al resto de los v¨¦rtices del grafo.
¡°En principio, el algoritmo podr¨ªa usarse para advertir a los actores, como los bancos centrales, si los especuladores est¨¢n especulando sobre la compra y venta de varias monedas. Mucho de esto sucede usando computadoras hoy en d¨ªa. Pero debido a que nuestro algoritmo es tan r¨¢pido, podr¨ªa ser capaz de para ser utilizado para detectar lagunas antes de que sean explotadas¡±, indica Christian Wulff-Nilsen.

